Introduction

C# is a great and mature programming language. In general, the whole .NET environment which I work with on a daily basis is extremely developer friendly – things like Rider (IDE), NuGet (package manager) etc. work like a charm. However, few weeks ago I started to get into details of cryptography stuff and corresponding math related topics (I even completed Stanford Online course in this regard). The math behind cryptography schemes tends to rely on large numbers (hundreds of digits) and uncommon math topics like modulo arithmetic and discrete logarithms. As I am most familiar with C# it was my first choice when it came to solve different puzzles and challenges. Thankfully, apart from standard integral types like int, long, ulong (ulong has the greatest possible positive value = 18,446,744,073,709,551,615) there is a struct called BigInteger which I used to learn how the Diffie-Hellman key exchange protocol can be broken. The protocol strength relies on the discrete logarithm problem (DLP). Of course this is for educational purposes only!

Diffie-Hellman key exchange

The Diffie-Hellman key exchange protocol was published in 1976. Long story shorts it was designed to establish a secret key between two parties over a public communication channel (public means that it could be eavesdropped – I don’t cover the exact details of the algorithm as there are many many well written explanation over the Internet). The protocol more or less looks like the following:

• Fix a large prime P (e.g. 600 digits).
• Fix an integer G such that G < P.
• Then:

To sum up, private component of the Diffie-Hellman protocol are: a, b, K, whereas public components are: P, G, A, B.

To find out what is the secret key K (remember, K = G^a*b mod P) we must find private values a and b. The a and b were used to generate publicly available A and B so maybe it would be a good idea to break them. To extract a from A and b from B we must win through a discrete logarithm problem. It basically states that if you know a, m and c it is hard to find b such that:

a^b=c mod m

If you look closer that is exactly what we want to get: a and b from A and B, i.e. G^a = A mod P and G^b = B mod P assuming we know G, B, A and P (which are publicly available).

Once we have the background of the problem the question is, how we can solve discrete logarithm problem? The most obvious idea is to brute force by checking a and b values starting from 1 up to the P-1. This method, however, is not feasible if we are talking about hundreds digit numbers. One way to ease the problem is to use baby step giant step algorithm.

Baby step giant step algorithm

The baby step giant step algorithm could be used to reduce the time complexity of the DLP from the linear complexity (O(N)) to the square root complexity (O(√N)) hence the time decreases dramatically. However, the algorithm is based on a space-time trade-off (there’s no such thing as a free lunch). You can find quite good explanation in the wiki page among others: baby step giant step algorithm so I don’t put it here. Instead, I present the implementation in C# and show some interesting benchmark.

Breaking DLP in C#

You can find the implementation of baby step giant step algorithm alongside the brute force implementation and benchmark of both on my GitHub:

• Implementation,
• Benchmark.

One thing that is unusual in my implementation is the limit argument in the Compute methods. This is a simplification of the algorithm because of my laptop limitation. For the sake of the blog post I limited the solution space by the limit argument so that is computationally feasible (the value of limit was chosen randomly, just to be greater than the solution of the DLP).

If you run the baby-step-giant-step (dotnet run, it takes ~30 sec) you can see that both algorithms (baby step giant step and brute force) find a solution.

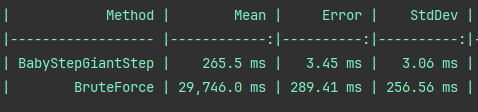
If you run the baby-step-giant-step-benchmark (dotnet run -c Release, it takes ~20 mins) you can see the following results:

Summary

In this post I presented the BigInteger API for dealing with really large numbers and the practical usage of the API – breaking the discrete logarithm problem. One thing I missed in the BigInteger API is a method for computing modulo inverse. I had to implement the extended Euclidean algorithm (BigIntegerExtensions class) to get such a modulo inverse (I followed this wiki page). Nevertheless, I am more than happy that there is such an API so that I can play with large number stuff in the language I am most familiar with. As always I encourage all of you to try it on your own!

Have a nice day, bye!