Introduction

Computing large numbers isn’t usually our day-to-day issue. We use multiplication when it comes to finding out how much of a paint would be enough to cover walls in our room. However, computers have to deal with multiplication and exponentiation on a regular basis. These days many cryptography formulae require to deal with large numbers computations. One of the key factor in cryptography is to make it fast and efficient enough so that it could be applied for an ordinary user.

Large exponentiation

Let’s consider the following example. We have an algorithm that at some point needs to compute the following: 7³⁰⁰⁰⁰. This is definitely a big number, however. Firs approach to that would be basic multiplication like 7 * 7 * 7 * … * 7 (30000 multiplications). It seems to be a good enough but as I’ve mentioned earlier the efficiency is crucial.

Now, let’s do the same but in a slightly different approach – using square and multiply algorithm. As you probably know from math classes the following formulae are true:

• 7¹¹ = 7 ¹⁰ * 7 ¹
• 7 ¹⁰ = 7 ⁵ * 7 ⁵

Having that in mind we can compute the 7 ³⁰⁰⁰⁰ as follows (I prepared a simple program that prints to operations for given base and exponent):

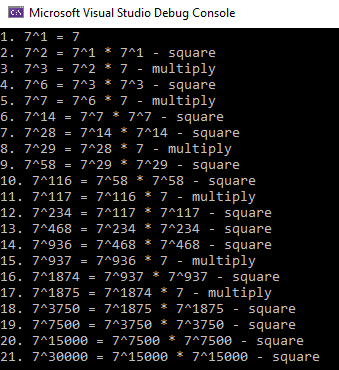
As you can see instead of 30000 multiplications we are able to do the same exponentiation in just 20 operations (we can ignore the first line)! I decided not to explain the algorithm in details

Summary

To sum up, the number of operations have a direct impact in terms of program performance. I didn’t explain here the exact algorithm’s steps as I believe that the above image explain the main idea of the algorithm well. I also encourage to read this Wikipedia page. Moreover, I’ve got inspired by this Computerphile video – I truly recommend this YouTube channel, there are many well-explained and interesting things to learn.

As always I’ve prepared an example and you can find it on my github, project: square-and-multiply.

Have a nice day, bye!