Introduction

Tree structure is extremely popular in the computer science. From time to time trees need to be traversed (i.e. visiting all the nodes) and there are three popular algorithms to do that:

• pre-order,
• in-order,
• post-order.

Each of them has its own use case and in this post I give a practical example of one use case for each algorithm. This time I implemented the solution in Haskell (first time here, hope not the last). My motivation for this topic is pretty straightforward – I believe it is much easier to remember and understand an algorithm if you know at least one usage of it. Without further ado, let’s go!

Note: I do not explain Haskell syntax nor internals in this post. However, you can check the code in my repo if you want to run locally or just look at it.

Pre-order

One of the use cases for the pre-order traversal algorithm is tree cloning. Let’s consider
a tree that we want to clone:

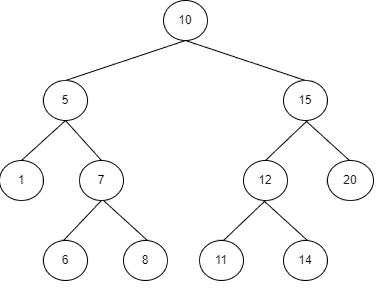
We can implement a tree cloning function using the following pseudocode:

1  Node Clone(Node existingNode){
2   if(existingNode == null){
3      return null;
4   }
5
6   newNode = new Node();
7   newNode.Value = existingNode.Value;
8   newNode.Left = Clone(existingNode.Left)
9   newNode.Right = Clone(existingNode.Right)
10
11  return newNode;
12 }

As you can see the cloning process clone the tree in a pre-order fashion:

1. Process a node – create a clone of the node with the proper value (line 6-7),
2. Go left – clone left subtree (line 8),
3. Go right – clone right subtree (line 9),
4. Once the function finishes it returns the root node.

In-order

Let’s talk a bit about in-order traversal algorithm and the same tree structure as the previous one:

If you look closer you can see that the tree has a unique feature – each and every left node has less value than the parent and each and every right node has greater value than the parent. If we have tree like this we can use the in-order traversal to get all the nodes in an ascending order -> [1, 5, 6, 7, 8, 10, 11, 12, 14, 15, 20].

Post-order

Last but not least algorithm is the post-order. This time let’s consider slightly different tree:

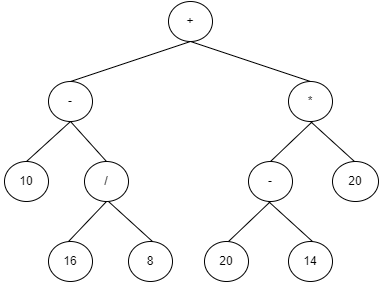
The tree represents abstract syntax tree of a simple arithmetic expression:
((10 – (16 / 8)) + ((20 – 14) * 20)). Interestingly, we can use the post-order to traverse the tree and compute the arithmetic expression – so let’s do it!

First, let’s use the post-order tree traversal and get all the nodes:
[10, 16, 8, /, -, 20, 14, -, 20, *, +]. What we get here is a collection of tokens that represents reverse polish notation. There are two types of tokens:

• values (e.g. 10, 16),
• operators (e.g. *, +).

The reverse polish notation is incredibly handy when it comes to compute e.g. an arithmetic expressions without using parenthesis. The algorithm to compute result from given tokens is simple and can be implemented based on the pseudocode (we consider here only valid collection of tokens):

int computeFromReversePolishNotation(List<Token> tokens){
   stack = new Stack<int>()

   foreach(token in tokens){
      if(isNumber(token)){
          stack.push(token);
      } else {
          rightOperand = stack.Pop()
          leftOperand = stack.Pop()
          operator = getOperator(token)
          r = compute(operator, leftOperand, rightOperand)
          stack.Push(r)
      }
   }

   return stack.Single()
}

Illustration of the algorithm:

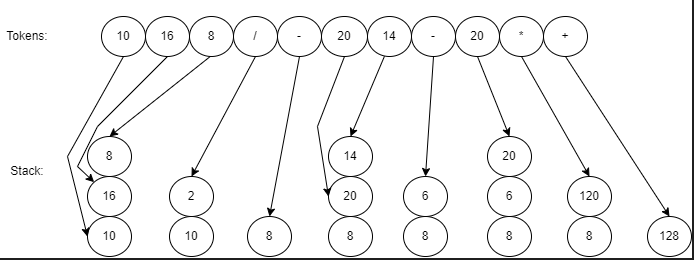
That’s pretty neat, isn’t it?

Summary

To sum up, in this post the three use cases of three different tree traversal algorithms are presented. Personally, I find it much easier to memorize an algorithm if I am aware of its use case. If you are interested in the implementation of the pre-order, in-order and post-order traversal algorithms in Haskell you can find the source code on my GitHub. Moreover, there are two implementations of reverse polish notation. The former one uses simple collection-as-stack approach whereas the latter implementation is based on a stack implemented with a state monad (inspired by this lecture).

Have a nice day, bye!